2021. 3. 10. 23:56ㆍ지식/수학
1. 평균(Mean)
- 어떤 변수의 합계가 고정되어 있을 때, 모든 관측치가 똑같이 나누어 가질 수 있는 값.
다 알고 있는 내용이지만 수식을 쓰자면 다음과 같다.

변수 x의 평균은 모든 관측치의 값을 다 더한 다음 관측치의 개수 n으로 나눠 계산한다.
평균의 표기법은 위와 같이 변수x에 "모두 같다"라는 의미로 "ㅡ"를 얹어 표기한다.
평균은 통계학에서 값의 상대적 위치를 알려준다. 내가 시험 점수가 60점이라고 했을 때
만약 평균이 30점이라면 내가 시험을 상대적으로 잘 본 것이고, 평균 이 80점이라고 했을 때
나는 상대적으로 시험을 못 본 축에 들게 되는 것이다.
2. 분산(Variance)
- Data의 서로 다른 관측치가 완전히 똑같은 값을 갖는 경우는 거의 없습니다.
거의 모든 Data의 관측치는 서로 다른 값을 갖습니다.
초기 통계학에서 이런 관측치가 평균에서 떨어져 있는 거리를 숫자로 계산하기 위해서
여러 가지 방법을 만들어 냈는데 그중 하나가 바로 '분산'입니다. 분산의 계산 식은 다음과 같습니다.

1) 각각의 관측치에서 평균을 뺸다. 관측치 별로 평균과의 차이를 계산.
2) 그 차이를 제곱한다. 차이가 '-'가 나왔든 '+' 값이 나왔든 그 차이를 확인하기 위함.
3) 그 값들을 모두 더한다.
4) 그 합계를 1 / (n-1)로 나눈다. 자유도라는 개념인데 이 후 포스팅에서 설명하겠지만
쉽게 변수의 값 중 하나가 평균과 차이가 없어 평균의 차이를 구했을 때 '0'에 가까운 값이
나오기 때문정도로 생각하면 된다.
5) 식을 보면 알겠지만 결국은 관측치와 평균의 차이의 평균을 구한 값.
즉, '평균에서 떨어져 있는 정도'
모든 관측치가 같은 값을 갖는다면 분산은 '0'이 나올 것입니다. 즉, 분산의 값이
'0'에 가까울 수록 관측치의 값들이 평균에 몰려 있다는 것을 의미합니다.
3. 표준편차(Standard Deviation)
- 통계학에서 관측치의 흩어져 있는 정도를 수치로 보기 위해 분산을 만들었지만,
우리는 분산을 잘 사용하지 않고 표준편차를 주로 사용합니다.
그 이유는 바로 단위 때문인데요. 위 분산의 계산식을 보면 알 수 있듯이
분산에서는 제곱이라는 수식이 들어가기 때문에 분산의 단위는 변수의 제곱이 되어 버립니다.
예를 들어 어떤 금액에 대한 분산을 구했는데 (원²) 이라는 듣도 보도 못한 단위가 생겨버리지요.
단위뿐만 아니라 제곱을 해버리기 때문에 차이의 값들도 커져버리게 됩니다.
만약, 내 투자금의 분산은 100000(원²)이야 라고 하면 직관적으로 차이가 느껴지나요?
그렇기 때문에 통계학에서는 이것들의 해결하기 위해 분산의 값에 제곱근(루트)을 해서
'표준편차'라는 것을 만들었습니다.
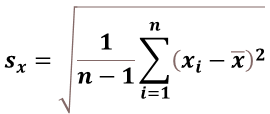
Standard Deviation의 앞글자를 따서 s라고 표현합니다.
'지식 > 수학' 카테고리의 다른 글
| [통계학] 분위수, 백분위수, 사분위수 (0) | 2021.03.03 |
|---|---|
| [통계학] 이변량 확률변수 (0) | 2021.02.17 |
| [통계학] 평균과 분산 (Expected Value , Variance Value) (0) | 2021.02.09 |